Polynomials

Definition of a polynomial

A polynomial is an expression made up of the sum of a finite number of powers in one or more variables multiplied by coefficients. This is a general polynomial in one variable:

$a_{n}x^{n}+b_{n-1}x^{n-1}+\ldots+a_{2}x^{2}+a_{1}x+a_{0}$

Each coefficient $ (a_{k}) $ would have a numerical value. The powers could start with any value of $ n $, and don’t need to include every power between $ n $ and $ 1 $. Here’s an example:

$2x^{4}-x^{2}+5x-9$

Polynomials can have multiple variables, and get a little more complicated. Here is an example of a polynomial with two variables:

$3x^{2}y^{2}+x^{2}y-2xy^{2}+4xy+x-2y+3$

This lesson will focus on polynomials with only one variable raised to powers of two or less, these polynomials have the form:

$a_{2}x^{2}+a_{1}x+a_{0}$

The coefficients $ (a_{2},a_{1},a_{0}) $ can be positive, negative, or zero. If you know the coefficients of a polynomial you can fully construct it, because the $ x $ terms stay the same. For example say:

$a_{2}=3,\;a_{1}=0,\;\text{and}\;a_{0}=-1$

Can you write the polynomial associated with these coefficients? It would be:

$(3)x^{2}+(0)x+(-1)\\=\;3x^{2}-1$

This lesson will focus on adding, subtracting, multiplying, and factoring polynomials.

Adding and subtraction polynomials

To add or subtract two polynomials you simply ‘combine like terms.’ This means that you add/subtract the coefficients of variables with the same power to get the new coefficients for those variables. For example, to add the polynomials $ 3x^{2}+6x-2 $ and $ x^{2}-4x+1 $ we would have:

$(3+1)x^{2}+(6-4)x+(-2+1)\\=4x^{2}+2x-1$

Subtraction works in the same way. Subtracting $ 2x^{2}+x-3 $ from $ -x^{2}-4x+5 $ gives:

$\begin{align*} & (-1-2)x^{2}+(-4-1)x+(5-(-3)) \\ & =-3x^{2}-5x+8 \end{align*}$

Take the same approach to add or subtract polynomials with two variables or more variables; however, you will have more terms to keep track of.

Adding $ x^{2}y^{2}-x^{2}y-3xy^{2}+2xy $ to $ 5x^{2}y^{2}+x^{2}y-2xy^{2}-6xy $ yields:

$\begin{align*} & (5+1)x^{2}y^{2}+(1-1)x^{2}y+(-2+-3)xy^{2}+(-6+2)xy \\ & =6x^{2}y^{2}-5xy^{2}-4xy \end{align*}$

Multiplying polynomials

We are only going to focus on multiplying simple polynomials of the form $ a_{1}x+1_{0} $. To multiply two polynomials you must multiply each term in the first polynomial by each term in the second polynomial and vice versa. The lines in the following picture connect terms that we must multiply together.

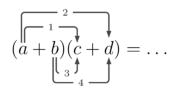
The below example illustrates this multiplicative distribution. After the multiplication, we combine like terms to reach a simplified solution.

$\begin{align*} & (x+1)(2x-3)= \\ & x(2x)+x(-3)+1(2x)+1(-3)= \\ & 2x^{2}-3x+2x-3= \\ & 2x^{2}-x-3 \end{align*}$

It is important to remember to multiply the $ x $ terms as well as the numbers. Below we show the solution to the general multiplication problem; you can think of it as a template into which real numbers can be substituted for the $ a $, $ b $, $ c $, and $ d $ terms.

$\begin{align*} & (ax+b)(cx+d)= \\ & (ac)x^{2}+(ad+bc)x+(bd) \end{align*}$

The key to multiplying polynomials is to make sure each term meets every other term once. Here is another example worth noting:

$\begin{align*} & (x+3)(x-3)= \\ & x(x)+x(-3)+3(x)+3(-3)= \\ & x^{2}-3x+3x-9= \\ & x^{2}-9 \end{align*}$

Factoring polynomials

Factoring a polynomial means decomposing it into the product of two smaller polynomials. For example:

$x^{2}-x-12 = (x-4)(x+3)$

Essentially we are working in the opposite direction as we were above when we multiplied small polynomials. The small polynomials $ x-4 $ and $ x+3 $ are said to be factors of the larger polynomial $ x^{2}-x-12 $.

Finding the factors of a polynomial requires a bit of guesswork and a familiarity with the process of polynomial multiplication that we discussed in the last section. I’ll refer to the general equation below while describing the process of factoring polynomials:

$ax^{2}+bx+c=(Ax+B)(Cx+D)$

When given an equation $ ax^{2}+bx+c $ and asked to factor it, you first need to choose $ A $ and $ C $ so that $ A\cdot C=a $. Then you need to choose $ B $ and $ D $ such that $ B\cdot D=c $ and $ (A\cdot D+B\cdot C)=b $.

As an example, say we want to factor the polynomial $ 2x^{2}+7x+3 $. We start by letting $ A=2 $ and $ C=1 $, since $ 2x\cdot1x=2x^{2} $. Now we must find $ B $ and $ D $ such that $ B\cdot D=3 $ and $ (2D+B)=7 $. This step usually involves some ‘guessing and checking.’ You should end up with $ B=1 $ and $ D=3 $. We now have all the pieces to factor our polynomial:

$2x^{2}+7x+3 = (2x+1)(x+3)$

You can check this factorization by multiplying the two factors; you should get the original polynomial as the answer. Factoring polynomials requires good intuition. It can get especially tricky when you have multiple possibilities for A and C, like when factoring $ 4x^{2}-9x+2 $. In this case we could have either $ A=4 $, $ C=1 $ or $ A=2 $, $ C=2 $. What you need to do is just pick one of the two options and then try to find $ B $ and $ D $. If you’re unable to find a $ B $ and $ D $ that work you need to switch to the other combination of $ A $ and $ C $. In this case the correct factorization is:

$4x^{2}-9x+2 = (4x-1)(x-2)$

Practice questions

Combine like terms

$ 2x^{2}-3x-4+3x^{2}+4x-1 $
$ 10a-6b-(2a-b) $
$ x^{2}y^{2}+4x^{2}y-4xy^{2}+xy+2x^{2}y^{2}-x^{2}y-2xy $
$ x^{2}-x-1-4(x^{2}-2x+1) $

Multiply and combine like terms

$ (x+1)(x-1) $
$ (3x-1)(2x+3) $
$ (2x-1)(1-x) $
$ (x+\frac{1}{2})(x+2) $
$ (2x-3)(2x+3) $
$ (x-4)^{2} $

Factor

$ x^{2}+4x+3 $
$ x^{2}-2x-8 $
$ x^{2}+12x+32 $
$ 2x^{2}+9x-5 $
$ 4x^{2}+20x+25 $
$ x^{2}-9 $
$ x^{2}+3x $
$ 2x^{2}+6x+4 $

Solutions

Solution: $$ \begin{align*} & 2x^{2}-3x-4+3x^{2}+4x-1= \\ & (2+3)x^{2}+(-3+4)x+(-4-1)= \\ & 5x^{2}+x-5 \end{align*} $$
Solution: $$ \begin{align*} & 10a-6b-(2a-b)= \\ & (10-2)a+(-6+1)b= \\ & 8a-5b \end{align*} $$
Solution: $$ \begin{align*} & x^{2}y^{2}+4x^{2}y-4xy^{2}+xy+2x^{2}y^{2}-x^{2}y-2xy = \\ & (1+2)x^{2}y^{2}+(4-1)x^{2}y-4xy^{2}+(1-2)xy = \\ & 3x^{2}y^{2}+3x^{2}y-4xy^{2}-xy \end{align*} $$
Solution: $$ \begin{align*} & x^{2}-x-1-4(x^{2}-2x+1)= \\ & x^{2}-x-1-(4x^{2}-8x+4)= \\ & (1-4)x^{2}+(-1+8)x+(-1-4)= \\ & -3x^{2}+7x-5 \end{align*} $$
Solution: $$ \begin{align*} & (x+1)(x-1)= \\ & x^{2}-x+x-1= \\ & x^{2}-1 \end{align*} $$
Solution: $$ \begin{align*} & (3x-1)(2x+3)= \\ & 6x^{2}+9x-2x-3= \\ & 6x^{2}+7x-3 \end{align*} $$
Solution: $$ \begin{align*} & (2x-1)(1-x)= \\ & 2x-2x^{2}-1+x= \\ & -2x^{2}+3x-1 \end{align*} $$
Solution: $$ \begin{align*} & (x+\frac{1}{2})(x+2)= \\ & x^{2}+2x+\frac{1}{2}x+1= \\ & x^{2}+\frac{5}{2}x+1 \end{align*} $$
Solution: $$ \begin{align*} & (2x-3)(2x+3)= \\ & 4x^{2}+6x-6x-9= \\ & 4x^{2}-9 \end{align*} $$
Solution: $$ \begin{align*} & (x-4)^{2}= \\ & (x-4)(x-4)= \\ & x^{2}-4x-4x+16= \\ & x^{2}-8x+16 \end{align*} $$
Solution: $$ \begin{align*} & x^{2}+4x+3= \\ & (x+1)(x+3) \end{align*} $$
Solution: $$ \begin{align*} & x^{2}-2x-8= \\ & (x+2)(x-4) \end{align*} $$
Solution: $$ \begin{align*} & x^{2}+12x+32= \\ & (x+8)(x+4) \end{align*} $$
Solution: $$ \begin{align*} & 2x^{2}+9x-5= \\ & (2x-1)(x+5) \end{align*} $$
Solution: $$ \begin{align*} & 4x^{2}+20x+25= \\ & (2x+5)(2x+5)= \\ & (2x+5)^{2} \end{align*} $$
Solution: $$ \begin{align*} & x^{2}-9= \\ & (x+3)(x-3) \end{align*} $$
Solution: $$ \begin{align*} & x^{2}+3x= \\ & x(x+3) \end{align*} $$
Solution: $$ \begin{align*} & 2x^{2}+6x+4= \\ & 2(x^{2}+3x+2)= \\ & 2(x+2)(x+1) \end{align*} $$

Previous Next